|
C*-Clifford algebra
|
(Definition)
|
|
|
Given a general Hilbert space
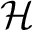 , one can define an associated , one can define an associated 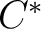 -Clifford algebra, -Clifford algebra,
![${\rm Cl}[\mathcal{H}]$ ${\rm Cl}[\mathcal{H}]$](http://images.physicslibrary.org/cache/objects/401/l2h/img3.png) , which admits a canonical representation on , which admits a canonical representation on
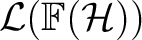 the bounded linear operators on the Fock space the bounded linear operators on the Fock space
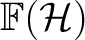 of of
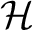 , (as in Plymen and Robinson, 1994), and hence one has a natural sequence of maps , (as in Plymen and Robinson, 1994), and hence one has a natural sequence of maps
![$\mathcal{H} {\longrightarrow}{\rm Cl}[\mathcal{H}] {\longrightarrow}\mathcal L(\mathbb{F}(\mathcal{H}))~. $ $\mathcal{H} {\longrightarrow}{\rm Cl}[\mathcal{H}] {\longrightarrow}\mathcal L(\mathbb{F}(\mathcal{H}))~. $](http://images.physicslibrary.org/cache/objects/401/l2h/img7.png)
The details and notation related to the definition of a 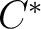 -Clifford algebra, are presented in the following brief paragraph and diagram. -Clifford algebra, are presented in the following brief paragraph and diagram.
Definition 0.1 Let us briefly recall the notion of a Clifford algebra with the above notations and auxiliary concepts. Consider first a pair 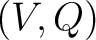 , where 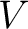 denotes a real vector space and  is a quadratic form on 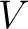 . Then, the Clifford algebra associated to  , denoted here as
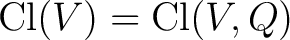 , is the algebra over
 generated by generated by  , where for all
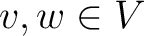 , the relations:
 are satisfied; in particular,
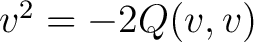 .
If 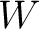 is an algebra and is an algebra and
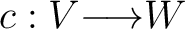 is a linear map satisfying is a linear map satisfying
 then there exists a unique algebra homomorphism then there exists a unique algebra homomorphism
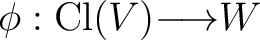 such that the diagram such that the diagram
Commutes. (It is in this sense that
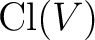 is considered to be `universal'). is considered to be `universal').
Then, with the above notation, one has the precise definition of the 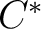 -Clifford algebra as -Clifford algebra as
![${\rm Cl}[\mathcal{H}]$ ${\rm Cl}[\mathcal{H}]$](http://images.physicslibrary.org/cache/objects/401/l2h/img27.png) when when
where  is a real vector space, as specified above.
Also note that the Clifford algebra is sometimes denoted as
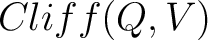 . .
|
"C*-Clifford algebra" is owned by bci1.
|
|
| Other names: |
Clifford algebra of quantum observables |
| Also defines: |
non-commutative algebra, quantum observable algebra (QOA) |
| Keywords: |
Clifford Algebra |
Cross-references: commutes, homomorphism, relations, vector space, concepts, Clifford algebra, diagram, linear operators, representation, Hilbert space
There are 3 references to this object.
This is version 1 of C*-Clifford algebra, born on 2009-01-15.
Object id is 401, canonical name is CCliffordAlgebra.
Accessed 1067 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

