|
Hilbert space
|
(Definition)
|
|
Definition 1.1 An inner-product space with complex scalars,
 , is a vector space  with complex scalars, together with a complex-valued function
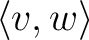 , called the inner product, defined on
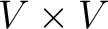 , which has the following properties:
Definition 1.2 A Banach space
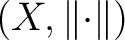 is a normed vector space such that 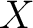 is complete under the metric induced by the norm
 .
Definition 2.1 A Hilbert space is an inner product space which is complete as a metric space, that is for every sequence 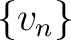 of vectors in 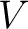 , if
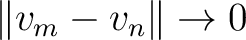 as 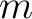 and  both tend to infinity, there is in 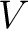 , a vector
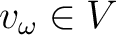 such that
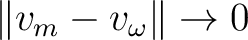 as
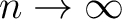 . (In quantum physics, all Hilbert spaces are tacitly assumed to be infinite dimensional)
Sequences with the property that
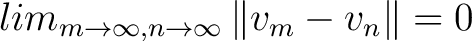 are called Cauchy sequences. Usually one works with Hilbert spaces because one needs to have available such limits of Cauchy sequences. Finite dimensional inner product spaces are automatically Hilbert spaces. However, it is the infinite dimensional Hilbert spaces that are important for the proper foundation of quantum mechanics. are called Cauchy sequences. Usually one works with Hilbert spaces because one needs to have available such limits of Cauchy sequences. Finite dimensional inner product spaces are automatically Hilbert spaces. However, it is the infinite dimensional Hilbert spaces that are important for the proper foundation of quantum mechanics.
A Hilbert space is also a Banach space in the norm induced by the inner product, because both the norm and the inner product induce the same metric.
|
"Hilbert space" is owned by bci1.
|
|
See Also: quantum groups and von Neumann algebras, topic on algebraic foundations of quantum algebraic topology, Poisson ring, vector space
| Also defines: |
Cauchy sequence, vector space, conjugate linear, inner product, norm, Banach space, metric space, metric induced norm, norm induced by inner product |
| Keywords: |
Hilbert space, quantum state space, norm, Banach space, vector space, Cauchy sequence, inner product, norm, Banach space, metric space, metric induced norm, norm induced by inner product |
Cross-references: quantum mechanics, works, vectors, metric, function, scalars
There are 62 references to this object.
This is version 38 of Hilbert space, born on 2009-05-21, modified 2009-05-21.
Object id is 768, canonical name is HilbertSpace3.
Accessed 5056 times total.
Classification:
|
|
|
|
|
|
|
|
Pending Errata and Addenda
|
|
|
|
|
|
|
|
|
|

